


■■■ トレモロユニットのスプリングばね定数を決める ■■■
レッドスペシャルの大きな特徴がトレモロユニットであることは疑いのない事実である。シンクロナイズドよりも複雑で、いかにもブライアン的な設計である(お父さんの設計かもしれないけど)。
今回Burnsを改造するにあたって、やはり一番大変なのがこのトレモロユニット作成である。なんてったって、何もないところから作り上げるのだからねぇ。ネットでみると、自分なりの解釈でこのトレモロユニットを作る方も多いのだが、私の場合、まずブライアンの基本構造を真似ることにした。しかし真似ると言っても、Burnsの構造上、ナイフエッジのプレートを表面薄板下に配置することなどまず無理である。そこは「安く作る」と「アイデアを出す」で乗り越えよう。
■■■ まずはオールドレディーのトレモロ構造を理解しよう ■■■
さて、まずは語りつくされた感はあるがオールドレディーのトレモロユニットの構造を整理しよう。
図1にボディー表面薄板をはいだ状態(そんな状態は作成途中以外しか見れないが)を示す。図2は同じアングルだが、片側のスプリング中心でカットモデルとした。図中Aがアームベース(B)の支点となるナイフ・エッジ・プレートである。アームダウンすると、アームベースB下部が左側に倒れ、スプリングを縮めるという仕組みである。スプリングを伸ばしてアームダウンするストラトとは全く違う構造なのが面白い。
ストラトの場合アームのトルク調整はスプリングの本数とスプリングフックの位置調整で行う(ちょっと原始的)だ。RSの場合はボディー下部ストラップピン横に開けられた「アクセスホール」から直接Dのボルトを回し、スプリング力を調節するという、工業的な仕組みである。
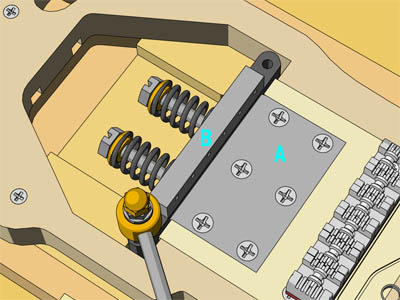
【図1】
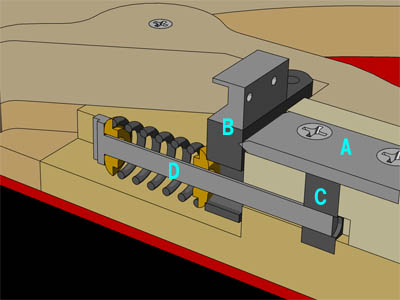
【図2】
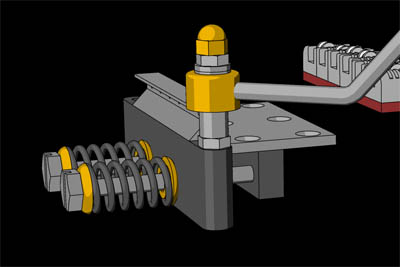
【図3】
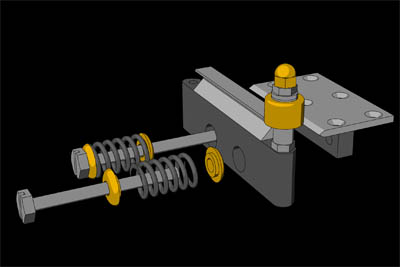
【図4】
■■■ コイルスプリングのばね定数 ■■■
【図5】
さて構造は見れば分かるので何とかなるが、なんともならないのがスプリングである。弦の張力とつり合いフローティング状態にするためには、このスプリングによる力を所定の値にしなければならない。トレモロポケットに構造一式を入れるため、スプリングの大きさ(コイル内外径、自由高さ、密着高さ)の制約がある。その制約の中で、所定の「ばね定数」を持つスプリングを探さなければならないのである。適当に選んでしまうと、たとえばばね定数が小さいと、スプリングが縮みきった状態になりアームダウンできなかったりするし、ばね定数が大きすぎると、アームダウンに過大な力がかかって構造が壊れちゃったりするだろう。
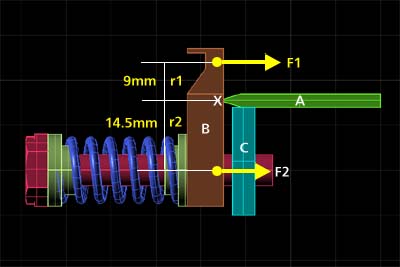
基本は図5を見てもらえば簡単に分かるだろう。小学生のてこの計算だ。トレモロをフローティング仕様とすれば、支点X(ナイフエッジ部)周りの回転モーメントがつりあえばよい。作用点はアームベースのストリングスエンドポスト(F1)と、コイルスプリングの中心線(F2)となる。ではおのおのの数値を見てみよう。
●弦張力
−609mm(24'')スケール
−弦径(インチ):009-042
−総合弦張力(1-6弦計):36.38kg
一般的に弦張力は T=(2Lf)^2xUw (T:弦張力、L:弦長、f:弦振動周波数、Uw:単位長あたりの弦質量)で求められる。しかしこの単位長あたりの質量Urなんてものは普通分からないのだ。なので、計算から張力を求めるのは即断念する。
しかし弦メーカーのD'Adarioのサイトには、いろいろな弦の張力が数値記載されている。これを利用しよう。。ここに掲載されているのは648mmスケールでの値だが、張力と弦長の関係は比例関係なので、648mmスケールの値に0.94を乗じてRSの609mmスケールの値とした。以下に各弦における値を示そう。
| Strigns | Diameter | Scale 25.5"/648mm | Scale 24"/609mm | freqency(Hz) | |||
| D(inch) | D(mm) | T(kg・f) | T(N) | T(kg・f) | T(N) | ||
| 6E | 0.042 | 1.0668 | 6.71 | 65.76 | 6.32 | 61.89 | 82.41 |
| 5A | 0.032 | 0.8128 | 7.17 | 70.27 | 6.75 | 66.13 | 110.00 |
| 4D | 0.024 | 0.6096 | 7.17 | 70.27 | 6.75 | 66.13 | 146.83 |
| 3G | 0.016 | 0.4064 | 6.67 | 65.37 | 6.28 | 61.52 | 196.00 |
| 2B | 0.011 | 0.2794 | 4.99 | 48.90 | 4.70 | 46.03 | 246.94 |
| 1E | 0.009 | 0.2286 | 5.94 | 58.21 | 5.59 | 54.79 | 329.63 |

【図5】
図5に示すよう、モーメント計算に必要な回転中心から作用点までの距離rは以下の通りだ。
r1(弦エンドポスト側):9mm
r2(スプリング側):14.5mm
以上より、弦張力による回転モーメントM1は以下の通り。
M1=36.38[kg] x 9.8[m/s^2] x 9[mm] = 3209[N・mm](一応国際標準にしたがってニュートンにしよう)
さてスプリングが上記回転モーメントM1と同等の力を出すためにスプリングに求められる力F2は、回転中心からの距離r2から以下の通り
F2 = M2/r2 = 3209[N・mm]/14.5[mm] = 221[N](22.6[kg])
つまりこの221[N](22.6kg・f)を2本のスプリング受け持つわけで、スプリング1本あたりはその半分の111[N](11.3kg・f)となる。

【図6】

【図7】
さてその辺に転がっていた強力そうなスプリング(図6)のばね常数を見てみると10[N/mm]と書いてある。ざっくり言えば11mm縮んで弦との平衡状態になるわけだ。
スプリングに求められる力が分かったので、現有スプリングがそれに合致するかを見てみよう。現有スプリングの仕様は一部実測の結果、以下のようになった。
−ばね定数:10[N/mm]
−コイル内外径:7.5/10[mm]
−自由高さ:28[mm]
−密着高さ:19[mm]
今回問題となったのが「密着高さ」であった。つまり縮み代が9mmしかない。フローティング状態で11mm縮んでくれなきゃいけないわけで、NGじゃん。ばねが弱すぎる。
というわけで、現時点(2010.2.13)でばね探し状態なのである。15N/mm位のばね見つけた人は連絡ください。
■■■ 原理モデル作成 ■■■
当初このスプリング周りの計算なんかしなかった。ずーっと不安だった。なので、ブライアント同じく原理モデルを作って簡単に確かめてみた。別途記載する「安価に作るトレモロ構造」の確認の意味もあったり、ちょうどフランケン作成用に買ったギターのネックが大量に余っていたし・・・
スケールも609mmに合わせたわけでなく、その変にあった適当な木材に取り付けただけである。でもこれでなんとなくスプリング力が足りないことがわかり、今回の計算に発展したわけだ。計算って大事である。

【図8】

【図9】

【図10】

【図11】